Introduction
Line symmetry is a fundamental principle in mathematics, design, and art. It is a concept that describes how an object or shape can be divided into two identical halves that mirror each other. When a shape or object is symmetrical, that means that the two halves are exactly the same or a perfect reflection of each other. In this article, we will explore the significance of line symmetry about the y-axis, and the importance of identifying which graphs exhibit y-axis symmetry. We will also provide an overview of how to determine if a graph shows line symmetry about the y-axis.
Exploring Line Symmetry
Line symmetry is the concept that describes when a shape or object can be divided into two identical halves that mirror each other along a line, thus resulting in a perfect reflection. It is represented by an imaginary line called the line of symmetry. When an object or shape is symmetrical, this means that it has at least one line of symmetry.
Examples of symmetrical shapes and objects include polygons, circles, and snowflakes. The symmetry present in these objects makes them visually appealing and balanced to the human eye.
Line symmetry has a broad range of applications in various fields. In mathematics, it is used to solve equations and problems involving graphs and shapes. In design, it is used to create aesthetically pleasing patterns, such as textiles or wallpaper. In art, it is used to create visually stunning compositions.
Y-Axis Symmetry
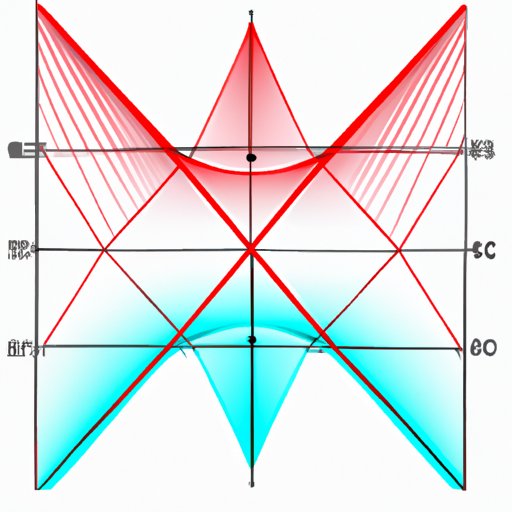
Y-axis symmetry describes when a graph is symmetrical with respect to the y-axis. It occurs when a graph is divided into two identical halves that mirror each other along the y-axis. The concept of y-axis symmetry is essential in mathematics, where it is used to solve problems related to algebraic equations, geometry, and calculus.
The y-axis symmetry characteristics of a graph can be identified by observing that the points on one side of the y-axis are equal to the corresponding points on the other side of the y-axis. When a graph is y-axis symmetric, it is identical to its mirror image on the other side of the y-axis.
Examples of graphs with y-axis symmetry include equations like y = x² and y = |x|.
Graphs that do not show y-axis symmetry are called asymmetrical. An asymmetrical graph has no mirror line that can divide it into two identical halves. In other words, the two halves of an asymmetrical graph are not a perfect reflection of each other along the y-axis.
The Magic of Line Symmetry
Identifying y-axis symmetry in graphs has various advantages and benefits. In mathematics, it simplifies equations and makes them easy to solve. In design, it creates balanced patterns that are aesthetically pleasing to the human eye. In art, it creates visually stunning compositions with spatial harmony and balance.
One benefit of identifying y-axis symmetry in graphs is that it helps to simplify the analysis of functions. When a graph is symmetrical with respect to the y-axis, it means that the function is even. This creates symmetry in the function about the y-axis, simplifying analysis and computation.
In design, y-axis symmetry helps to create balanced and harmonious patterns. It is commonly used in fashion design, textiles, architecture, and interior design. In art, it is used to create balanced and visually appealing compositions that have a strong impact on the viewer.
The concept of perfect reflections is also significant in various fields, including physics, optics, and astronomy.
Finding Perfect Reflections
To determine if a graph has y-axis symmetry, there are several steps to follow:
- Choose a point on the y-axis.
- Move the same distance to the left and right from the point on the y-axis.
- If the points on the left and right side of the y-axis are the same distance from the y-axis, then the graph is y-axis symmetric.
Another method to identify y-axis symmetry in a graph is to transform the graph using the y-axis symmetry formula. This formula replaces x with -x in the equation of the graph. If the equation does not change after substituting x with -x, the graph is y-axis symmetric.
Finally, the visual inspection method is useful in identifying y-axis symmetry in graphs. When a graph is y-axis symmetric, it appears as a mirror image along the y-axis.
Symmetrical Graphs Made Easy
Identifying y-axis symmetry in graphs can be challenging, and it requires practice and persistence to master the skill. Some common mistakes to avoid include:
- Incorrectly identifying the y-axis as the x-axis or the origin.
- Incorrectly substituting the incorrect values for x or -x in the equation of the graph.
- Ignoring or failing to see the symmetry present in the graph.
Some strategies to make the process of identifying y-axis symmetry in graphs more manageable include:
- Practicing on different graphs until you get the hang of it.
- Breaking down the graphs into different parts to see if each half has symmetry.
- Visualizing the symmetry of the graph instead of relying solely on the equations.
With practice and persistence, identifying y-axis symmetry in graphs will become an intuitive process.
The Beauty of Y-Axis Symmetry
In conclusion, line symmetry about the y-axis is a fundamental concept in mathematics, design, and art. It is the principle that describes how shapes can be divided into two identical halves that mirror each other along a line. Identifying y-axis symmetry in graphs requires practice and persistence. The process involves choosing a point on the y-axis, moving the same distance left and right from that point, and comparing the points to determine if they are the same distance from the y-axis.
Identifying y-axis symmetry in graphs has various advantages and benefits, including simplifying equations, creating aesthetically pleasing patterns, and producing visually stunning compositions. Identifying the perfect symmetry represented by perfect reflections is important in many fields, including physics, optics, and astronomy.
Overall, understanding line symmetry about the y-axis is a valuable skill that has numerous applications and is essential in many fields of study and design.